be gone, dual y-axis!
Due to popular demand (and a growing waitlist for the sold out workshop on 2/3!), I've scheduled another upcoming workshop in San Francisco on 2/8. Details & registration here.
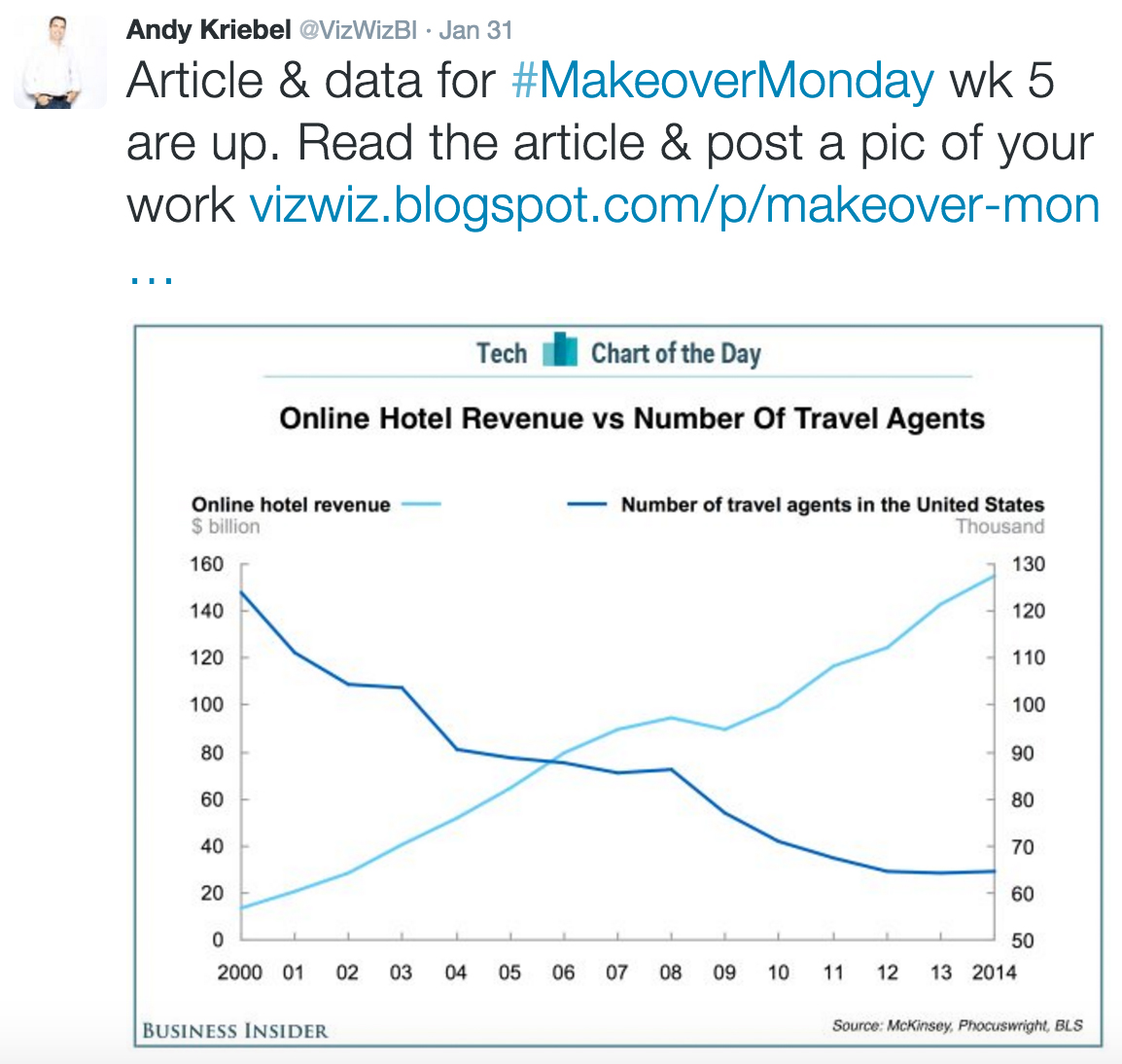
I am generally not a fan of the dual y-axis. I've written about it before and offered some alternatives in my book and here. When scrolling through my Twitter feed last night, I came across the following offender and couldn't resist trying to improve upon it and taking part in the #MakeoverMonday challenge.
Before we get to the graph, let me spend a moment on #MakeoverMonday. This is a weekly segment that Andy Kriebel has been doing for quite some time (he's a busy guy; check out another fun current project of his with Jeff Shaffer, Dear Data Two). The premise is simple: take a less than stellar graph and make it better. In 2016, he's adding to the fun by doubling the Andys (having Andy Cotgreave join him) and also opening it up to the public. I think this is an awesome way to get people involved, share best practices and ideas, and generally inspire.
OK, back to the graph. The main challenge with a secondary y-axis is that there's always some questioning up front about which data to read against which axis. This particular example isn't horrible in that regard—the left and right orientation of Online hotel revenue and Number of travel agents titles, respectively, make it fairly clear which axis is which (though it does feel a little strange that each title is closest in proximity to the other data series, not the one it describes) . This graph does have another issue introduced by the secondary y-axis, however: the appearance of a crossing of the lines between 2005 and 2006. This looks like it might be something noteworthy, but actually is only a function of the scale used on the axes that creates a condition that they happen to cross each other at that point. Different scales would have them crossing in different places. I'd argue that they shouldn't cross at all.
In my workshops and book, when the topic of the secondary y-axis arises, I generally focus on two alternatives: 1) not showing the second (right-hand) y-axis but rather labeling the data in the secondary series directly or 2) pulling the graphs apart vertically so you can still leverage the same x-axis across both, but each gets its own left-hand y-axis so you can title and label them directly. Today, I thought I'd focus on a third potential alternative: turning the data that would be on two separate y-axes into the same units so you can simply plot it all on the same axis.
"Thought" in the preceding sentence is key. I'd envisioned my solution and penned the majority of this post before graphing the data (I've been doing this long enough that I should have recognized the danger in this). I thought I had the perfect solution in mind, but then graphed it only to recognize, "oops, that doesn't work." So let me rework the rest of this post. I'll take you briefly through my failed iteration and thought process as I do so.
Back to the idea of making the units the same and plotting it all on a single axis: this won't always be possible or appropriate, but I think (thought) it may work well in this case. For me, the point of this graph is that online hotel bookings have increased hugely over the past 15 years and that this has been—understandably—accompanied by a marked decrease in the number of travel agents. Since we're talking about increases and decreases here, one way to tackle would be to transform the numbers into relative increases and decreases and plot those directly. Here's what that could look like:
I hadn't looked at the numbers closely before graphing this, so failed to realize that the increase in online hotel bookings waaaay outpaces the decrease in travel agents. This totally makes sense now that I pause to think about it. But before seeing it, I was imagining a graph where online hotel bookings would be going upward to the right (as they are) and travel agents would be following perhaps a similar trajectory but downward to the right. The issue is that when scaled properly, the percent decrease in travel agents is totally dwarfed by the increase in online hotel bookings, so you don't really get a lot of value from the slightly downward sloping line (which also gets covered up in an unideal way by the x-axis labels).
Before seeing this, I was planning to discuss how moving from real numbers (for example, revenue or number of agents) to a percent (in this case, % change) causes you to lose something (sense of scale of overall numbers). I was then planning to go on to show a couple different ways to overcome this—first, by adding numbers to the graph directly, second by showing the actual numbers over time as well in bars (with number of travel agents being plotted in the negative direction) but pushing the bars to the background so they add a bit of context without a lot of clutter and maintain focus on the percent change. But none of this discussion makes much sense now that my original graph doesn't work.
Rather, after seeing the numbers graphed and recognizing just how huge the increase in online hotel bookings has been over the past 15 years, I'd be apt to just focus on that. The travel agent decline can become more of an interesting tidbit, included through use of text (not graphed at all). It isn't exactly the eloquent solution I was imagining, but it's where I'm going to land this time:
Be sure to check out Andy K and Andy C's respective solutions (here and here) where they go through more iterations and potential solutions for reimagining the original dual-axis graph. Interestingly, they both ultimately landed on scatterplots. For me, this does something strange to the dimension of time, but with adequate labeling (or animation, as Andy C uses), perhaps this is overcome. Take a look and see what you think.
By the way, if you're looking to hone your data visualization skills, consider participating in a future #MakeoverMonday challenge. I'll be following along. I hope to see your contribution there!